Quanti anni ha la Terra?

Cerchiamo di rispondere a questa domanda introducendo il fenomeno del decadimento radioattivo a cui vanno incontro gli elementi.

1 Quanti anni ha la Terra?

La Terra ha circa 4,4 miliardi di anni. 44 milioni di vite umane, 900 mila vite dell’albero più antico del mondo (un pinus longaeva), 140 milioni di miliardi di secondi… Senti l’orologio che ticchetta?

La domanda è: come facciamo a dirlo? Quale orologio è così antico da aver contato per noi così tanti anni?

Risposta: gli atomi! Ci sono atomi di determinati elementi che hanno tempi di dimezzamento così lunghi da consentirci di datare eventi lontanissimi nel tempo, come la nascita della Terra stessa. Vediamo in dettaglio come funziona.

2 Tempo di dimezzamento

Gli atomi decadono. Inizia tutto da qui, da questo fenomeno naturale, il decadimento. Gli atomi non sono fermi, immobili ed immutabili, ma cercano continuamente di mettersi in una posizione di migliore stabilità. I decadimenti possono essere di vario tipo, generati da cause diverse, ma non li analizziamo adesso, ci limitiamo a descriverne il funzionamento generale: gli atomi si trasformano in atomi più stabili emettendo energia e/o determinate particelle che dipendono dal tipo di decadimento.

Considerato un campione di un certo elemento, il tempo di dimezzamento è il tempo che impiega la metà del campione a decadere, a trasformarsi in un altro elemento.

2.1 Facciamo un esempio:

L’Uranio $_{92}^{238}U$ decade con un tempo di dimezzamento di $4,47 \cdot 10^9$ anni, trasformandosi in Torio $_{90}^{234}Th$, con espulsione di una particella $\alpha$

$$_{92}^{238}U \rightarrow \space _{90}^{234}Th + \alpha$$

Il Torio a sua volta decade, in quanto ancora instabile. Si ha così una catena di decadimenti detti serie radioattiva, che porta ad un atomo stabile. In questo caso ci fermiamo al Piombo $_{82}^{206}Pb$:

$\space$

$\space$

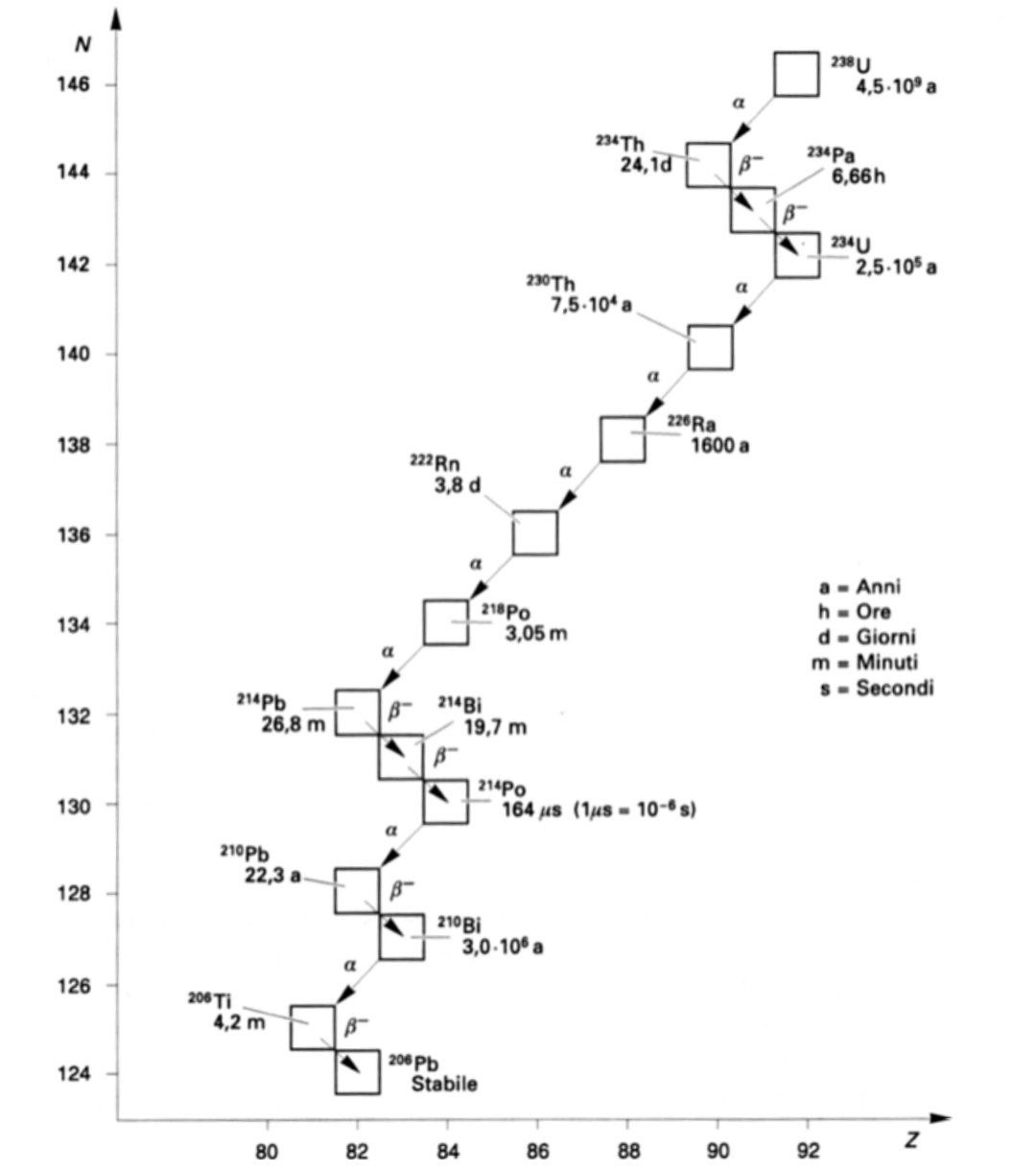
Visto che gli altri decadimenti hanno un tempo di dimezzamento molto minore rispetto al primo, si può dire che l’atomo instabile di Uranio 238 decade in un atomo di Piombo 206 con un tempo di dimezzamento di $4,47\cdot10^9$ anni.

In generale, ogni isotopo elementare ha il suo tempo di dimezzamento:

3 Dunque

Guardando la tabella ci rendiamo subito conto del fatto che alcuni elementi hanno un tempo di dimezzamento confrontabile se non superiore all’età della Terra! È proprio analizzando la quantità di materiale decaduto di questi elementi all’interno delle rocce che riusciamo a risalire all' età di formazione delle rocce stesse. Ricercando questa età per le rocce supposte più antiche, si ottiene il valore attuale di 4,4 miliardi di anni.